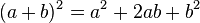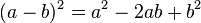Pitágoras.
Nació : alrededor del 580 AC en Samos, Ionia.
Falleció : alrededor del 500 AC en Metapontum, Lucania.
Era originario de la isla de Samos, situado en el Mar Egeo. En la época de este filósofo la isla era gobernada por el tirano Polícrates. Como el espíritu libre de Pitágoras no podía avenirse a esta forma de gobierno, emigró hacia el occidente, fundando en Crotona (al sur de Italia) una asociación que no tenía el carácter de una escuela filosófica sino el de una comunidad religiosa. Por este motivo, puede decirse que las ciencias matemáticas han nacido en el mundo griego de una corporación de carácter religioso y moral. Ellos se reunían para efectuar ciertas ceremonias, para ayudarse mutuamente, y aun para vivir en comunidad.
Se debe a Pitágoras el carácter esencialmente deductivo de la Geometría y el encadenamiento lógico de sus proposiciones, cualidades que conservan hasta nuestros días.La base de su filosofía fue la ciencia de los números, y es así como llegó a atribuirles propiedades físicas a las cantidades y magnitudes. Es así como el número cinco era el símbolo de color; la pirámide, el del fuego; un sólido simbolizaba la tetrada, es decir, los cuatro elementos esenciales: tierra, aire, agua y fuego.

 , se conoce com trinomio cuadrado perdfecto;
, se conoce com trinomio cuadrado perdfecto;