DIOFANTO ALEJANDRIA:
Nació: alrededor del año 200
Murió: alrededor del año 284
La obra más conocida de Diofanto es Aritmética, una colección de 130 problemas, distribuidos en 13 libros, de los que sólo se conservan 6. La mayoría de los problemas son de ecuaciones lineales y cuadráticas, pero siempre con solución positiva y racional, pues en aquella época no tenían sentido los números negativos y mucho menos los irracionales.
Diofanto consideró tres tipos de ecuaciones de segundo grado:
ax2 + bx = c
ax2 = bx + c
ax2 + c = bx
El motivo de no considerar estas ecuaciones como una sola es que en aquella época no existía el cero ni los números negativos.
Personajes historicos de las matematicas
Etiquetas: personajes 0 comentariosPublicado por Bloodless en 14:01
Mejora tu interaccion con la red
Etiquetas: consejos 0 comentariosEl rincon de las matematicas recomienda usar Mozilla Firefox
Publicado por Anónimo en 17:35
se recomienda...
Etiquetas: consejos 0 comentariosse recomienda hacer 5 ejercicios diarios en el siguiente orden:
-facil
-facil
-dificil
-dificil
-mediana dificultad
esto es para cada tipo de materia(potencias, notacion cientifica, etc.)
Publicado por Anónimo en 17:18
Algebra
Etiquetas: materia 0 comentariosEl álgebra es una rama de las Matemáticas que estudia la forma de resolver las ecuaciones.
Una de las características del álgebra es que utiliza símbolos para representar números.
El álgebra actual trata con entidades mas generales que los números y sobre estas entidades define operaciones (similares a las operaciones aritméticas). Esta nueva álgebra se debe a Galois.
Ecuaciones
Una expresión algebráica es una combinación de números y símbolos (que representan números). Por ejemplo: 5x2 + 3x3y3z.
Un término es una combinación de números y símbolos (que representan números) unidos por operaciones de multiplicación o división. Por ejemplo: 5x2, 3x3y3z son los términos de la expresión algebraica 5x2 + 3x3y3z.
Un factor es cada uno de los componentes de un término. Por ejemplo: 5 y x2, son los factores del término 5x2 de la expresión algebráica 5x2 + 3x3y3z .
Elegido un factor, un coeficiente, es lo queda del término. Por ejemplo: 3 es el coeficiente de x3y3z, x3 es el coeficiente de 3y3z, z es el coeficiente de 3x3y3 y así sucesivamente. Si el coeficiente es un número se le llama coeficiente numérico.
Dos términos se dice que son similares cuando sólo se diferencian en el coeficiente numérico.
El grado de un término es la suma de los exponentes de las variables. Por ejemplo: el grado del término 3x3y3z es 7. El grado de una constante es cero.
Las ecuaciones son igualdades. Nunca debemos olvidar esto.
Debemos distinguir entre identidades y ecuaciones. Cuando dos expresiones son iguales para cualesquiera valores que se pongan en lugar de las letras que figuran en la expresión es una identidad. Cuando la igualdad sólo se cumple para determinados valores de la expresión es una ecuación.
Por ejemplo: 2x2 + 5x2 + x2 = 8x2 es una identidad y 2x2 + 3x = 5 es una ecuación.
Las ecuaciones se pueden clasificar de varias formas:
a) Por el número de incógnitas.
Las ecuaciones pueden tener una o más incógnitas. Por ejemplo la ecuación 3x + 4 = 10, sólo tiene una incógnita, la ecuación 3x - y = 5, tiene dos y 5xy - 3x2 + z = 8 tiene tres incógnitas.
b) Por el grado de la incógnita.Las ecuaciones de una incógnita se pueden clasificar por el grado de la incógnita (el grado es el exponente más alto de la incógnita).Hay fórmulas generales para resolver las ecuaciones de grado 1 a 4 (pero las fórmulas son complicadas y difíciles de recordar para grado mayor que 2).
c) Por el número de términos
c1]Ecuaciones binómicas:
Las ecuaciones con dos términos se llaman ecuaciones binómicas.c2]Ecuaciones polinómicas:
PROBLEMAS PROPUESTOS
PROBLEMAS RESUELTOS
Publicado por Alejandro en 10:49
MATEMATICAS de Microsoft 2007
Etiquetas: software 0 comentariosExcelente programa que resuelve tus problemas matemáticos en un instante y paso por paso asta con que formula tendría el programa que resolverlo.
Entre estos instrumentos se incluyen:
Resolución de ecuaciones paso a paso
Esta herramienta ofrece a los estudiantes soluciones graduales con muchos problemas de matemáticas propios de la enseñanza media y superior, incluyendo: Álgebra, Geometría, Trigonometría y Aritmética.
Excelente calculadora gráfica en dos y tres dimensiones
Esta potente herramienta funciona de manera más eficiente que muchas calculadoras al uso que cuestan hasta 100€. El trabajo puede guardarse a la mitad para terminar más tarde, añadirse a documentos Word o PowerPoint o compartido entre grupos de estudio.
La calculadora gráfica también ofrece:
- Herramientas para convertir fórmulas científicas y ecuaciones matemáticas en gráficas, desde las matemáticas más simples al cálculo infinitesimal.
-Tecnología tridimensional
-Aspecto externo personalizable
Resolución de triángulos
Este instrumento desarrolla capacidades de geometría. Ahora los estudiantes pueden introducir fácilmente sus propios valores.
La calculadora:
-Determina la información desconocida
-Dibuja el triángulo a escala
-Provee las reglas matemáticas usadas para calcular los valores que faltan.
Fórmulas y ecuaciones
Este componente contiene más de 125 ecuaciones matemáticas y fórmulas de uso común e interactivas. Cuando los estudiantes introduzcan los datos, la biblioteca proporcionará la variable que falla y muchas veces también un gráfico de la ecuación.
Conversor de unidades
Esta herramienta resulta sumamente útil tanto en matemáticas como en ciencias al facilitar a los estudiantes la rápida conversión de unas unidades de medida a otras en magnitudes como: Longitud,área, volumen, peso, temperatura, presión, energía, potencia, velocidad y masa.
DESCARGA AQUÍ
Publicado por Alejandro en 18:33
Notación científica
Etiquetas: materia 1 comentariosLa notación científica (o notación índice estándar) es un modo de representar un conjunto de números -ya sean enteros o reales-mediante una técnica llamada coma flotante aplicada al sistema decimal, es decir, potencias de base diez. Esta notación es utilizada en numeros demasiado grandes o demasiado pequeños. La notación científica es utilizada para reducir cantidades muy grandes, y que podamos manejar con más facilidad.
Escribir un número en notación científica es expresarlo como el producto de un número mayor o igual que 1 y menor que 10, y una potencia de 10.
Operaciones matemáticas con notación científica
Adición
Siempre que las potencias de 10 sean las mismas, se debe sumar las mantisas, dejando la potencia de 10 con el mismo grado (en caso de que no tengan el mismo exponente, debe convertirse la mantisa multiplicándola o dividiéndola por 10 tantas veces como sea necesario para obtener el mismo exponente):
Ejemplo: 5·106
Multiplicación
Se multiplican los coeficientes y se suman los exponentes:
Ejemplo: (4·105)·(2·107) = 8·1012
División
Se dividen los coeficientes y se restan los exponentes (numerador_denominador):
Ejemplo: (4·1012)/(2·105) =2·107
Potenciación
Se potencia la mantisa y se multiplican los exponentes:
Ejemplo: (3·106)2 = 9·1012
Radicación
Se debe extraer la raíz de la mantisa y dividir el exponente por el índice de la raíz:
Ejemplo: 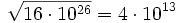
Publicado por Alejandro en 13:57
Extraccion de la raiz cuadrada
Etiquetas: materia 0 comentariosVoy a explicar el procedimiento para hallar la raíz cuadrada inexacta de un número por medio de un ejemplo ilustrativo.
Ejemplo ilustrativo:
Hallar la raíz cuadrada de 623 y expresar el resultado con dos cifras decimales.


















Publicado por Alejandro en 10:43
Importante
Etiquetas: consejos 0 comentariosEs posible que estés en busca de ejercicios resueltos de Matemáticas y también es posible que hayas recorrido bastantes sitios web y todavía no encuentras realmente lo que buscas. Es muy normal que ésto así ocurra, por una razón muy simple. En los sitios que regalan ejercicios resueltos de Matemáticas, aparecen los ejercicios impuestos por la persona que allí los habilitó y quizás de suerte a tí te sirvan. Puedes llenar tu computador con ejercicios que tal vez estén muy lejos de lo que tu profesor está interesado en evaluarte, como también llenar tu computador con muchos ejercicios que tal vez nunca estudies. Quizás convenga que te prepares con materia y ejercicios al estilo que tu profesor considera importante, ¿ no crees?.
Publicado por Alejandro en 10:32
Propiedades de las pòtencias
Etiquetas: materia 2 comentarios
Producto de potencias de igual base
Para multiplicar potencias de igual base, ponemos la misma base y sumamos los exponentes.
Ejemplo: 2 3x 2 5 = (2x2x2) x (2x2x2x2x2) = 2 8 = 2 3+5 (como la base (2) es la misma, los exponentes se suman) y da como resultado = 2 3+5 = 256
División de potencias de igual base
Cuando queremos dividir potencias que poseen la misma base, debemos restar los exponentes.
Ejemplo: 2 5:2 2 = (2x2x2x2x2) : (2x2) =2 5-2 = 2 3= 8
Potencia de un producto
Si queremos realizar la siguiente operación: (2x3) 3 observamos que (2x3) 3 = (2x3) x (2x3) x (2x3) = (2x2x2) x (3x3x3) = 2 3 x 3 3.
Para calcular el resultado también podemos multiplicar (2x3) y elevar el producto al cubo: (2x3) 3 = 6 3 = 216 O bien, elevar al cubo cada uno de los factores, que sería: 2 3 = 8 y 3 3 = 27 y luego, multiplicar el resultado: 8 x 27 = 216.
Decimos entonces que la potencia de un producto es igual al producto de la potencia.
Potencia de un cociente
La potencia de un cociente es igual al cociente entre la potencia del dividendo y la del divisor.
Tenemos que elevar el dividendo y el divisor a dicha potencia. Ejemplo: (6:2) 2 = 6 2: 2 2 = 9; Porque: (6:2) 2 = 3 2 = 9
Potencia de una potencia
Para elevar una potencia a otra potencia, debes poner la misma base y luego multiplicar los exponentes.
Ejemplo:
(2 2) 3 = 64; porque: 2 2 x 2 2 x 2 2 = 2 x 2 x 2 x 2 x 2 x 2 = 64 ; o también podemos multiplicar los exponentes: es decir, 2 x 3 y, luego elevar la base a dicho resultado.
Mira el ejemplo: (2 2x3) = 2 6= 64
Publicado por Alejandro en 10:07
Diseño e iconos por N.Design Studio | A Blogger por Blog and Web

